3RRP Mechanism — Kinematic & Dynamic Analysis
A full symbolic + numerical study of a 3-RRP planar parallel manipulator: closed-form kinematics, workspace / isotropy metrics, and Kane- vs-Lagrange dynamics validated in Simulink.
1 · Overview & Motivation
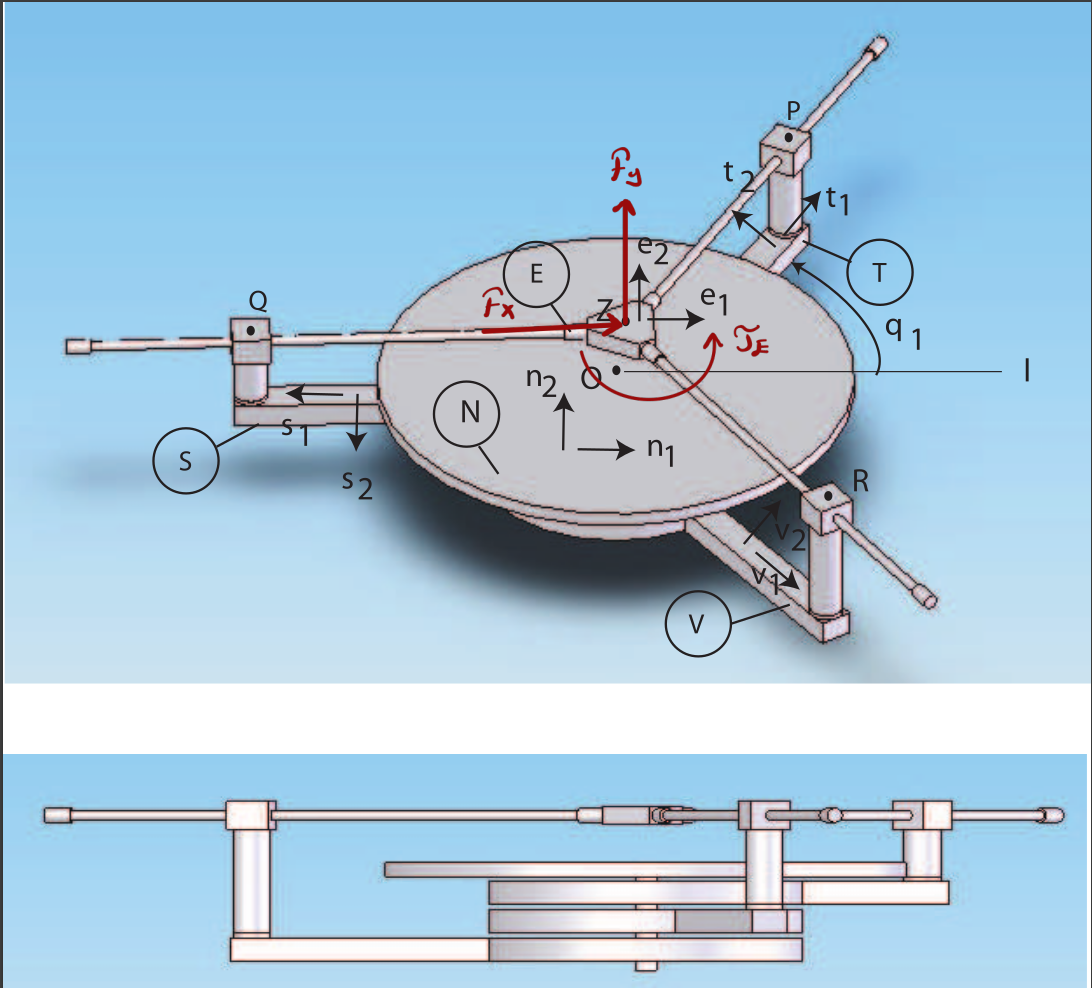
The 3-RRP planar parallel manipulator offers high stiffness and full planar dexterity using three revolute–revolute–prismatic legs.
Between Oct 2024 – Jan 2025 (EE 521 · Kinematics & Dynamics of Machines, Sabancı University) I performed an end-to-end analysis to
- derive closed-form forward & inverse kinematics,
- map the largest symmetric workspace and its Global Isotropy Index (GII),
- formulate equations of motion with Kane’s and Lagrange (Baumgarte-stabilised) methods, and
- validate both models in MATLAB / Simulink under small force & torque perturbations.
2 · Modeling Workflow
| Stage | Toolchain | Outcome |
|---|---|---|
| Symbolic kinematics | Autolev + manual algebra | Closed-form FK / IK |
| Workspace sampling | MATLAB (parfor) | ≈ 230 mm-radius reach |
| Isotropy metric | MATLAB · SVD(J) | GII = 0.46 |
| Dynamics (Kane) | Autolev → MATLAB | Compact ODEs |
| Dynamics (Lagrange) | Autolev + λ, Baumgarte | DAE system |
| Validation | Simulink | Stable under 0.001 N/N·m |
Pipeline Snapshot
3 · Key Results
| Metric | Value / Observation |
|---|---|
| Workspace | Circular, R ≈ 230 mm (link length 200 mm) |
| Global Isotropy Index | 0.46 (min σ / max σ) |
| Dynamics drift | < 0.5 % state error over 5 s |
| RHS eval (Kane) | ~20 µs (MATLAB R2024a) |
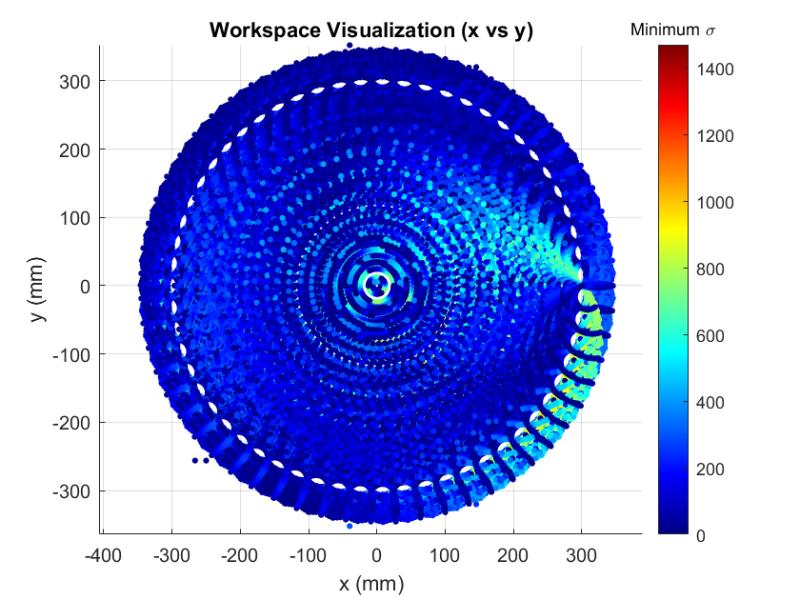
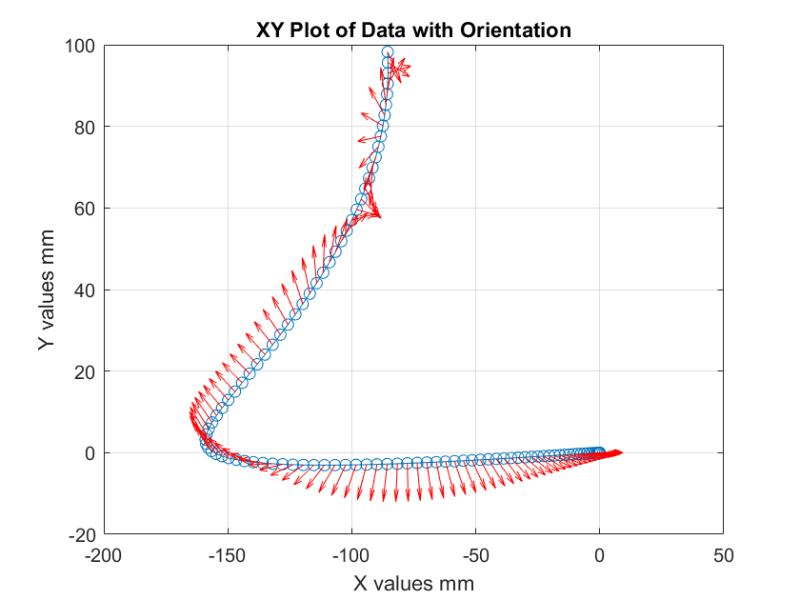
L → R: Workspace scatter; end-effector trace under 0.001 N (−X); isotropy distribution.
4 · Kane vs Lagrange — Quick Take
| Aspect | Kane’s Method | Lagrange + λ |
|---|---|---|
| Constraint handling | Implicit (partial velocities) | Explicit multipliers |
| Symbolic length | Shorter | Longer |
| Numerical stiffness | Low | Moderate (α, β tuning) |
| Physical intuition | Force / velocity | Energy focus |
| Best use | Real-time control | Energy shaping |
5 · Deliverables & Next Steps
- Simulink library – drag-and-drop FK, IK, Jacobian, dynamics blocks
- MATLAB scripts – workspace & isotropy samplers, disturbance demos
- Full PDF – derivations, listings, discussion
Future work: add joint friction & compliance, design Jacobian-weighted impedance control, and build a benchtop prototype for hardware correlation.
Solo term project for EE 521 — Kinematics & Dynamics of Machines (Fall 2024, Sabancı University).